yupsung Computer Science blog

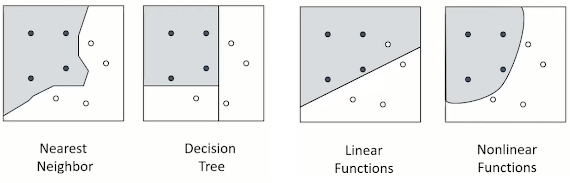
02_4 : Kernel based learning : Support Vector Regression (SVR) 앞에서 공부했던 SVM은 binary classification을 하기 위한 방법이었다. 이번 글에서 알아볼 SVR은 함수를 추정하여 연속적인 수치변수를 예측하는 회귀 방법이다.  SVR을 알아보기에 앞서 우리가 하려는 함수추정의 목적을 살펴보자. Fitting function 함수를 추정하고 싶을 때 우리의 목적은 크게 2가지로 나뉜다. Minimize an error measure (Loss function) 한마디로 error를 최소화 하여야 한다. (잘 맞춰야 한다) Function to be simple 같은 성능이라면, 함수는 최대한 단순해야 한다. 함수가 단순하다는 뜻은 아래의 조건들을 의미한다. Fewest basis functions Simplest basis functions Flatness is desirable Support Vector Regression (SVR) 위에서 살펴보았던 Loss function과 Flatness를 반영하도록 목적함수를 만들 것이다. SVR에도 여러 종류가 있는데, 우선 $\varepsilon$-SVR에 대하여 알아보자. 현실의 Data들은 어쩔 수 없이 발생하는 noise가 존재한다. 아래 식에서 noise는 $\varepsilon$이다. $$y = f(x)+\varepsilon$$ $\varepsilon$-SVR에서 핵심 아이디어는 $\varepsilon$ 보다 작은 noise에 대해서는 Loss를 주지 말자는 것이다.  왼쪽 그림에서 색이 칠해진 영역을 Epsilon-tube 라고 하는데, 이 영역안에 있는 객체들에게는 Loss를 부여하지 않는다. 이를 위한 Loss function은 오른쪽에 표현된다. 이 Loss function은 hinge를 닮았다고 해서, Hinge Loss 라고 불린다. 차이가 $\varepsilon$ 보다 작은 경우 loss는 0이고, $\vareps...

02_3 : Kernel based learning : Support Vector Machine (SVM) - Soft margin 이전 글에서는 Hard margin을 사용하는 SVM에 대하여 알아보았다. 이번에는 Soft margin을 사용하는 경우를 알아보자.  SVM - Case 2 : Linear case & Soft margin 지금까지는 분류경계면에 대하여 margin을 넘어가는 객체가 없다고 가정하고 Hard margin을 적용하였다. 하지만 실제 데이터에는 noise가 존재하기 때문에 위와 같은 경우가 발생하기 마련이다. 위의 경우에 Hard margin을 사용하면 분류경계면의 생성이 불가능하다. 그래서 모든 객체가 margin의 밖에 존재해야 한다는 제약을 제거하고 margin 안쪽에도 존재할 수 있도록 예외를 허용해주는 방법이 Soft margin이다. 물론 margin 안쪽에 존재하는 경우를 그냥 허용하는 것이 아니라 Penalty를 준다.  위 예시에서 $\xi$에 해당하는 값이 error 객체에 대한 Penalty이다. Penalty를 부여하는 방법에 따라 C-SVM과 nu-SVM으로 나뉘는데, 이 글에서는 C-SVM에 대하여 알아볼 것이다. Optimization problem (C-SVM) - Objective function $$ min\;\;\;\;\frac{1}{2}||\textbf{w}||^2+C\sum_{i=1}^N\xi_i $$ - Constraints $$ s.t.\;\;\;\;y_i(\textbf{w}^T\textbf{x}_i+b)\geq 1-\xi_i,\;\;\;\xi_i\geq 0,\;\;\forall i$$ Objective function의 $\frac{1}{2}||\textbf{w}||^2$은 기존의 Hard margin에서 사용했던 Margin이 최대화 되도록 한다. 그리고 위에서 말했던 Penalty를 주는 부분이 $C\sum_{i=1}^N\xi_i$식이다. 이 식을 통해 예외를 허...

02_2 : Kernel based learning : Support Vector Machine (SVM) - Linear & Hard margin Discriminant Function in classification Binary Classification 문제가 주어졌을때 classification을 수행하는 방법은 크게 4가지가 있다. 우리가 이번에 공부해볼 Support Vector Machine (SVM)은 이 중 Linear Function $g(\textbf{x})=\textbf{w}^T\textbf{x}+b$을 사용한 Classification 방법이다. Binary Classification Problem 우선은 우리가 해결할 Binary classification 문제를 정의해보자. Training data Sample drawn i.i.d from set $X\in\mathbb{R}^d$ according to some distribution D $$S=\{(x_1,\,y_1),\,(x_2,\,y_2),\,\cdots ,\,(x_n,\,y_n)\} \in X \times \{-1,+1\}$$ i.i.d는 independent and identically distributed를 뜻한다. binary classification임으로 각 class를 구분하는데, 0, 1이 아니라 +1과 -1로 구분하는 이유는 SVM의 수학적 formulation을 좀더 간략히 하기 위해서이다. Problem Find hypothesis $h\;:\;X\rightarrow \{-1,+1\}$ in H(classifier) with small generalization error $R_D(h)$ 구조적 위험 최소화 관점에서 일반화 된 error $R_D$를 최소화 하는 분류기 H를 만드는 것이 목표이다. 또한 SVM은 linear classifier임으로 고차원 상에서 high-dimensional data를 분류하는 Hyperplane을 찾는것이 목표이다....

02_1 : Kernel based Learning : Theoretical Foundation 이번 글에서는 Kernel 기반 알고리즘의 이해를 위해 기본적으로 필요한 개념을 공부해 볼 것이다. Shatter "A set of points is said to be shattered by a class of functions if, no matter how we assign a binary label to each points, a member of the class can perfectly separate them." 위의 정의를 살펴보면, 개별적인 각각의 point에 대하여 가능한 모든 binary label을 할당 하였을때 어떤 함수 F를 사용해 모든 point의 구분이 가능하다면, 이 point들의 집합을 Shatter 되었다 고 한다. 어떤 직선 분류기(linear classifier)가 있고, 직선 분류기에 의해 구분되는 Class를 +1, -1라고 생각하자. 그렇다면 이러한 직선 분류기를 사용하여 한 점을 +1, -1로 표현 가능하다. 그렇다면 직선 분류기를 사용하여 두 점의 모든 경우를 표현할 수 있을까? 다음과 같이 4개의 직선 분류기를 사용하면 각 직선 분류기가 각각의 A, B 두 점의 경우의 수를 표현한다. 따라서 모든 경우의 수를 표현 가능하다. 이처럼 함수 F에 대하여 n개의 point를 임의의 +1, -1을 Target value로 하는 분류 경계면의 생성이 가능하면, 함수 F가 n개의 point를 Shatter 할 수 있다고 한다. 2차원 상의 점 3개도 직선 분류기를 사용하여 모든 경우의 수($2^3 = 8$가지)를 표현 가능하다. 그렇다면 2차원 상에서 점 4개를 직선 분류기를 사용하여 모든 경우의 수($2^4 = 16$가지)를 표현 가능할까? 14개의 경우를 표현 가능하지만, 우측 하단의 두 경우를 표현하지 못한다. (이 두 경우는 XOR 문제라고도 불린다) 직선 분류기는 각 차원마다 최대 몇개의 점을 Sha...